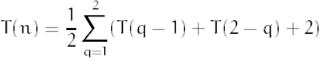CS502 Solved Mid Term Paper by Arslan Ali

Question No: 1    ( Marks: 1 )    – Please choose one

 Random access machine or RAM is a/an

► Machine build by Al-Khwarizmi

► Mechanical machine

► Electronics machine

       ► Mathematical model

Question No: 2    ( Marks: 1 )    – Please choose one

 _______________ is a graphical representation of an algorithm

►  notation

► notation

       ► Flowchart

► Asymptotic notation

Question No: 3    ( Marks: 1 )    – Please choose one

 A RAM is an idealized machine with ______________ random-access memory.

► 256MB

► 512MB

       ► an infinitely large

► 100GB

Question No: 4    ( Marks: 1 )    – Please choose one

 What type of instructions Random Access Machine (RAM) can execute? Choose best answer

► Algebraic and logic

► Geometric and arithmetic

       ► Arithmetic and logic

► Parallel and recursive

Question No: 6    ( Marks: 1 )    – Please choose one

 What is the solution to the recurrence T(n) = T(n/2)+n .

 

► O(logn)

       ► O(n)

► O(nlogn)

► O(n²)

Question No: 7    ( Marks: 1 )    – Please choose one

 Consider the following code:

For(j=1; j<n;j++)

For(k=1; k<15;k++)

For(l=5; l<n; l++)

{

Do_something_constant();

}

What is the order of execution for this code.

       ► O(n)

► O(n³)


► O(n² log n)

► O(n²)

Question No: 8    ( Marks: 1 )    – Please choose one

 Consider the following Algorithm:

Factorial (n){

   if (n=1)

      return 1

   else

       return (n * Factorial(n-1))

 

}

Recurrence for the following algorithm is:

► T(n) = T(n-1) +1

► T(n) = nT(n-1) +1

► T(n)= T(n-1) +n

       ► T(n)=T(n(n-1)) +1

Question No: 9    ( Marks: 1 )    – Please choose one

 What is the total time to heapify?

► Ο(log n)

► Ο(n log n)

► Ο(n² log n)

► Ο(log² n)

Question No: 10    ( Marks: 1 )    – Please choose one

 When we call heapify then at each level the comparison performed takes time

       ► It will take Θ (1)

► Time will vary according to the nature of input data

► It can not be predicted

► It will take Θ (log n)

Question No: 11    ( Marks: 1 )    – Please choose one

 In Quick sort, we don’t have the control over the sizes of recursive calls

       ► True

► False

► Less information to decide

► Either true or false

Question No: 12    ( Marks: 1 )    – Please choose one

 Is it possible to sort without making comparisons?

       ► Yes

► No

Question No: 13    ( Marks: 1 )    – Please choose one

 If there are Θ (n²) entries in edit distance matrix then the total running time is

► Θ (1)

       ► Θ (n²)

► Θ (n)

► Θ (n log n)

Question No: 14    ( Marks: 1 )    – Please choose one

 For Chain Matrix Multiplication we can not use divide and conquer approach because,

► We do not know the optimum k

       ► We use divide and conquer for sorting only

► We can easily perform it in linear time

► Size of data is not given

Question No: 15    ( Marks: 1 )    – Please choose one

 The Knapsack problem belongs to the domain of _______________ problems.

       ► Optimization

► NP Complete

► Linear Solution

► Sorting

Question No: 16    ( Marks: 1 )    – Please choose one

 Suppose we have three items as shown in the following table, and suppose the capacity of the knapsack is 50 i.e. W = 50.

The optimal solution is to pick


► Items 1 and 2

► Items 1 and 3

       ► Items 2 and 3

► None of these

Question No: 17    ( Marks: 2 )

 Describe an efficient algorithm to find the median of a set of 10⁶ integers; it is known that there are fewer than 100 distinct integers in the set

Question No: 18    ( Marks: 2 )

 How we can avoid unnecessary repetitions for recursive calls?

Question No: 19    ( Marks: 2 )

 Draw the cost table for chain matrix multiplication problem with initial state.

Question No: 20    ( Marks: 3 )

 Solve it,

 

Question No: 21    ( Marks: 3 )

 What are Catalan numbers? Give the formula.

Question No: 22    ( Marks: 5 )

What is the effect of calling Max-Heapify(A, i) when i > heap-size[A]/2?

Question No: 23    ( Marks: 5 )

 Write the pseudo code for 0/1 knapsack algorithm developed using dynamic programming technique.